Project 2 Adaptive Bitrate Streaming-Model Predictive Control
Author: Zhen Tong 120090694
Preface
This is a computer network course second project in CUHKSZ. We are asked to reproduce one algorithm for the Adaptive Bitrate problem. And this document is write for MPC(2015 SIGCOMM) reproduction.
Problem Definition
Video Streaming Model
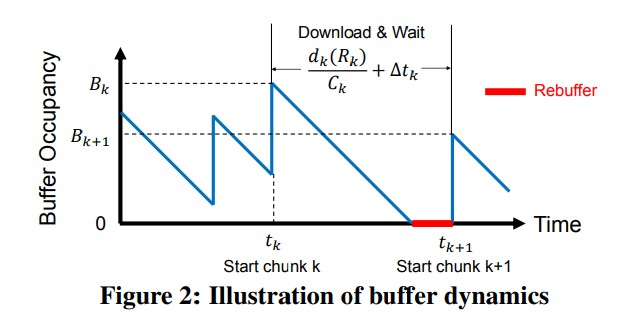
The model is transmit by means of chunks
With a higher bitrate
We can write the download process in the buffer formally:
In this function,
After the one chunk
QoE Maximization Problem
Another goal is improve the QoE of users. This project provides a flexible QoE.
Average video quality a measurement of the whole video, averaging the quality of all chunks.
Average Quality Variations is a measurement to consecutive variation of the quality, which cares about the sequential quality fluctuation.
Total rebuffering time is the sum of rebuffering for each chunk downloading. We want to minimize this measurement
Startup Delay
Every user have different preference therefore, the
In the paper, researchers use 3 sets of weights:
Balanced:
Avoid Instability:
Avoid Rebuffering:
MPC Algorithm
Our goal is to design a good function
Obviously, using the rate-based function
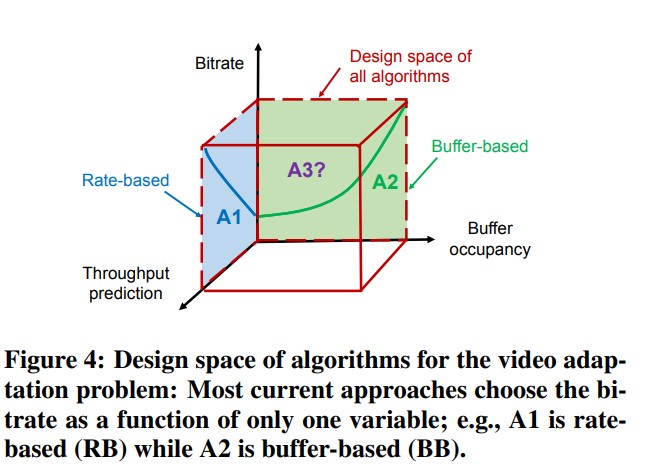
The intuition here is that network conditions are reasonably stable on short timescales and usually do not change drastically during a short horizon (tens of seconds). Based on this insight, we can run a QoE optimization using the prediction in this horizon. Focusing the horizon between
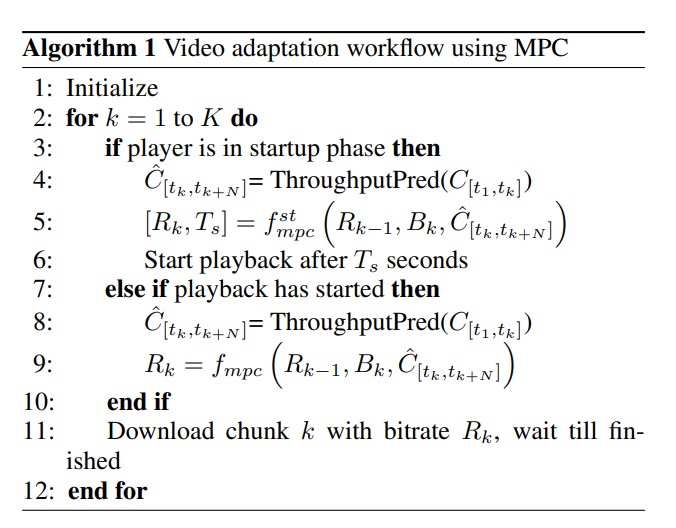
Because this paper is not focus on the predictor function, they refer to the previous work(click to see paper), and use the harmonic mean of the observed throughput of the last 5 chunks because it is robust to outliers in per-chunk estimates
The core optimization in this algorithm is:

Change into dynamic programming
Although this problem can be solved as a integer programming, it can be also solved directly using dynamic programming. Further, the quality of the bitrate is not explicitly write out in the paper, which is understandable because the user experience varies. However, to write the code, I simply take log for
Performance
Because this algorithm has the benefit over simply buffer-based approach or simply rate-based approach, in the performance part, we test the average bitrate, buffer time, and switch stability between MPC and buffer-based (BB) algorithm. Apparently, when the trace is ALT, the MPC is better than BB.
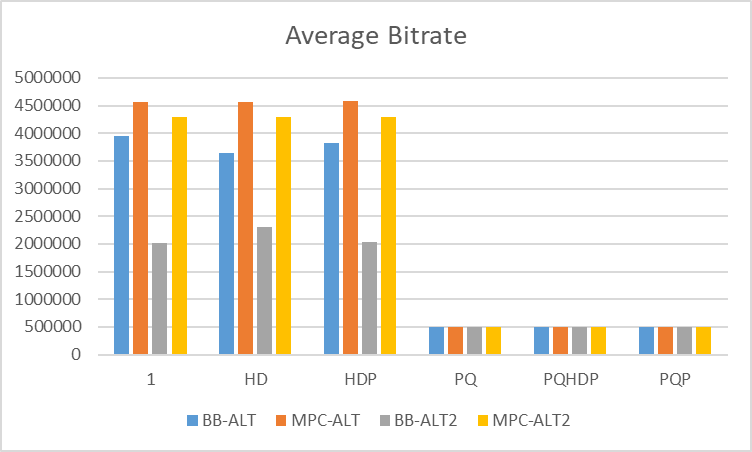
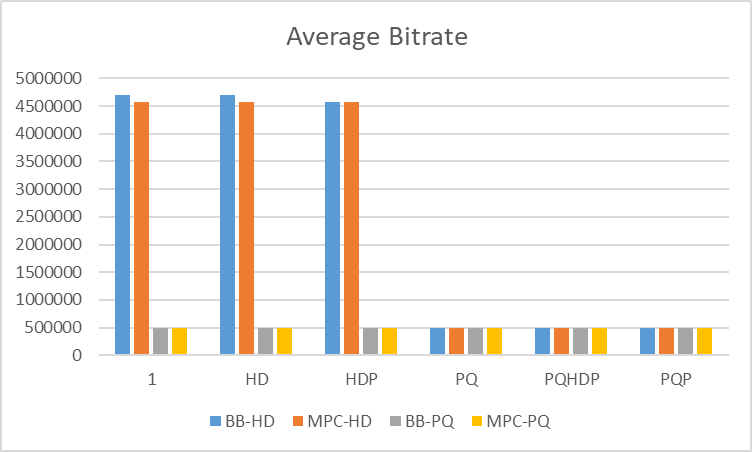
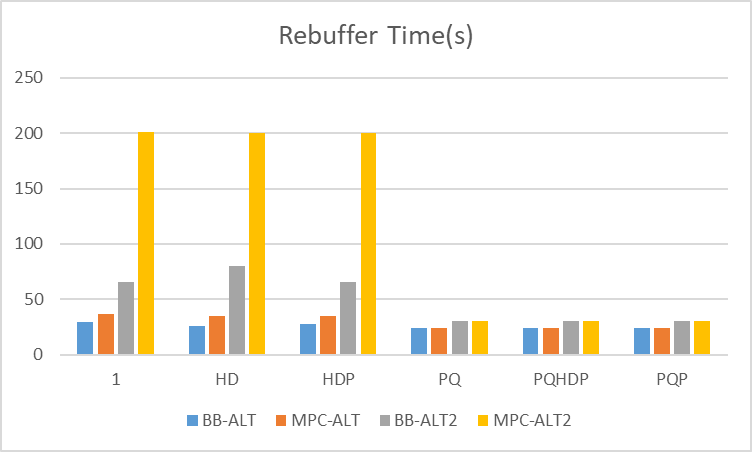
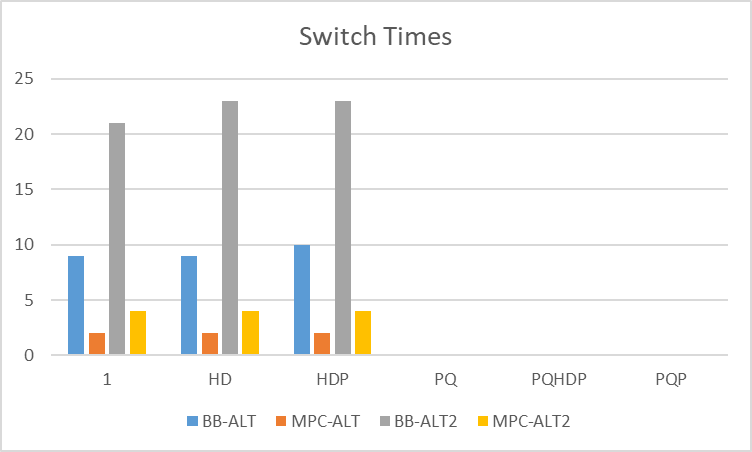
As for the rebuffer time, because the most of the time, MPC will offer a better bitrate, which means it will take more time to download the video. As for the HD and PQ trace, the rebuffering time is pretty the same. Because the MPC has one target to make the quality of video stable, from the switch times graph, we can see the MPC has less switch times than the BB algorithm
How to Run
There are a batch of simulation files list in the run_simulation.sh waiting for you to run. Only uncomment one line to test one case, don't test all! This is because the simulation need to communicate with the BBComm.py or mpComm.py
xchmod +x scripts/run_simulation.shchmod +x scripts/run_BB.shchmod +x scripts/run_MPC.sh
Then first run the scripts/run_BB.sh or scripts/run_MPC.sh in one terminal, and run the scripts/run_simulation.sh in another terminal. You can also run the code without bash. But I recommend you do that because it can show you the detail performance in the log.txt.
Reference
Yin, Xiaoqi, et al. "A control-theoretic approach for dynamic adaptive video streaming over HTTP." Proceedings of the 2015 ACM Conference on Special Interest Group on Data Communication. 2015.
Jiang, Junchen, Vyas Sekar, and Hui Zhang. "Improving fairness, efficiency, and stability in http-based adaptive video streaming with festive." Proceedings of the 8th international conference on Emerging networking experiments and technologies. 2012.
Huang, Te-Yuan, et al. "A buffer-based approach to rate adaptation: Evidence from a large video streaming service." Proceedings of the 2014 ACM conference on SIGCOMM. 2014.