An Improved Algorithm for Traditional Image Inpainting

Author: Songlin Zhao, Zijin Cui, Zhen Tong

Motivation

The technology of image inpainting is widely used today. There are many traditional algorithms to achieve that. However, most of them suffer from low speed because of pixel-by-pixel iteration. Besides, due to the roughly designed mask, some information of the original image is lost. Moreover, it can only propagate the texture and structure information in the original input image to fill the blank region. In our project, we propose an improved algorithm, trying to tackle these flaws.

Goal

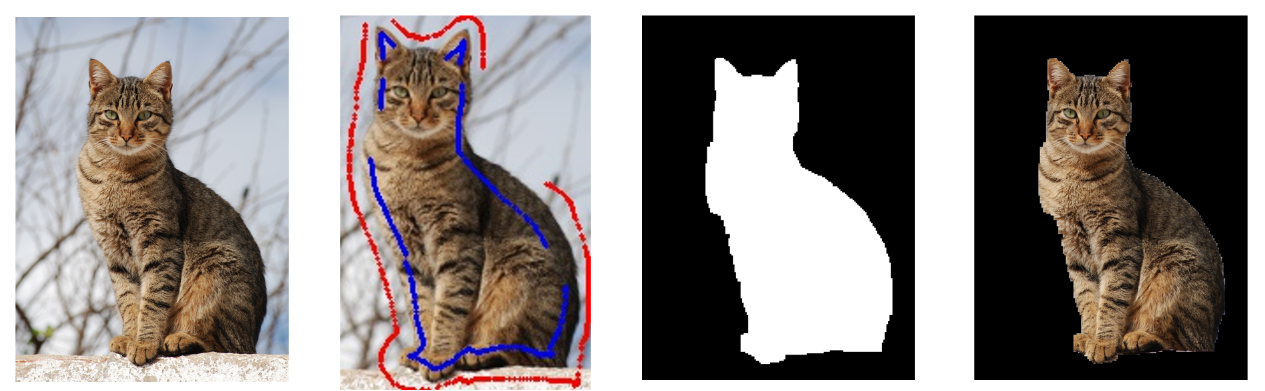
Given an image with an unwanted object, mask the unwanted object and fill the mask region.

Pipeline

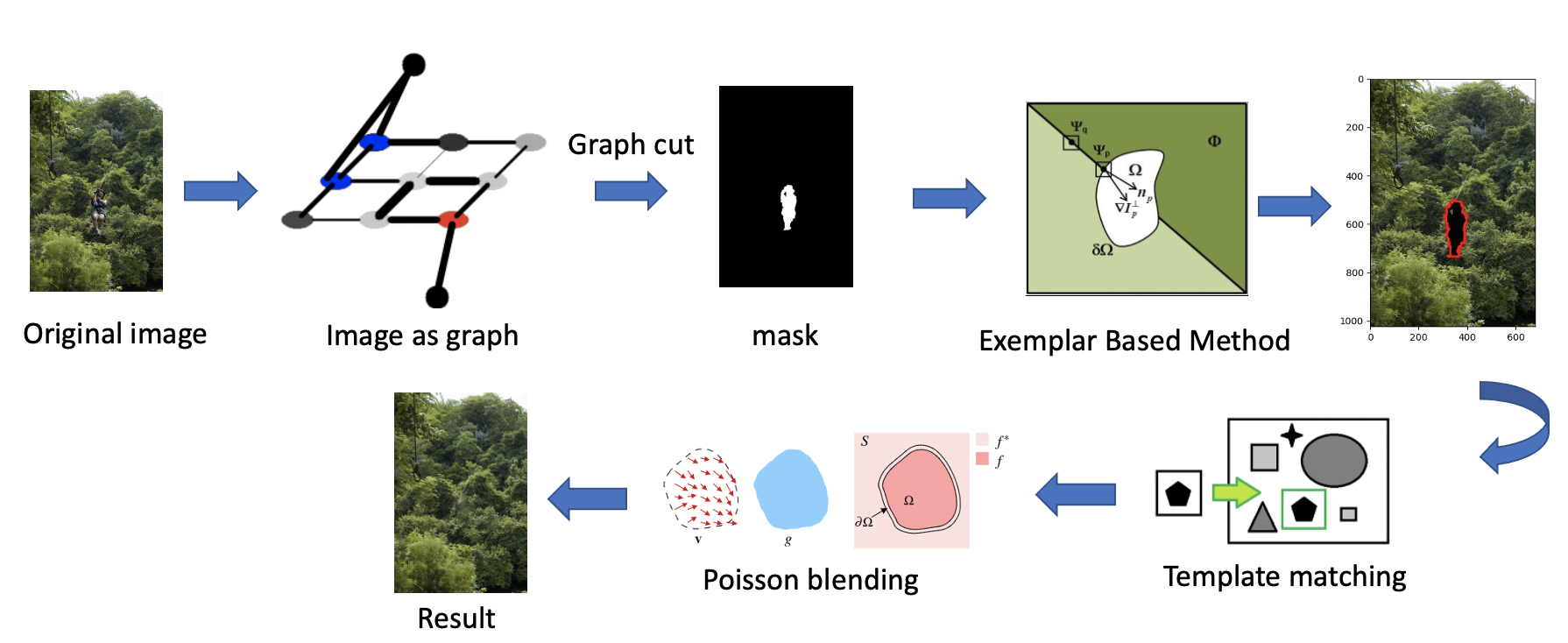
Methodology

Segmentation Using Graph Cuts

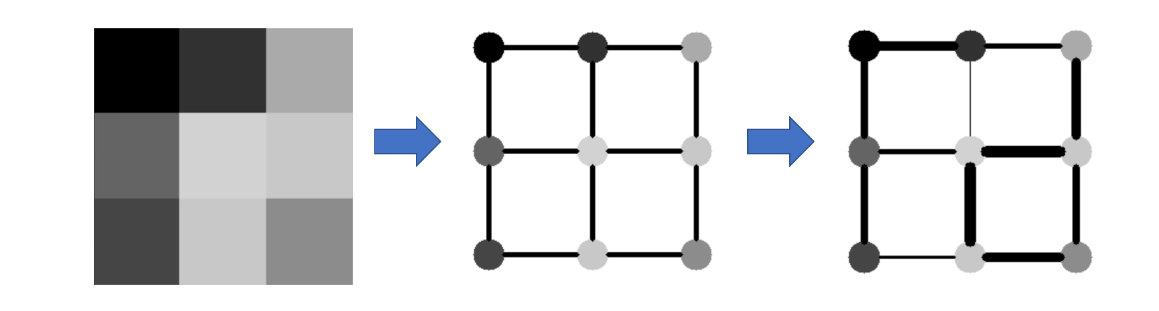
Image as a graph

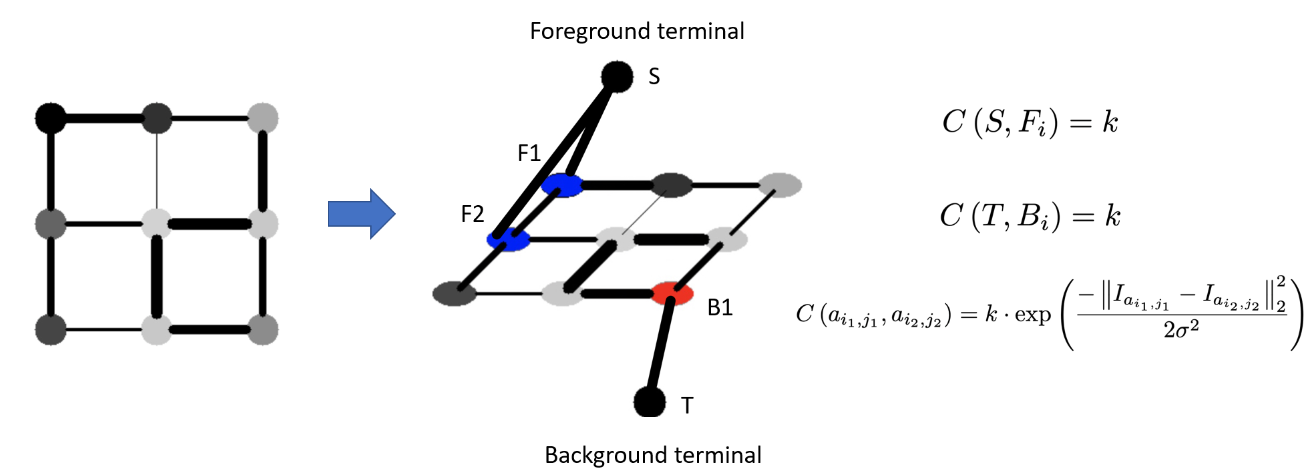
Graph cut using Ford-Fulkerson Algorithm

Exemplar fill iteration

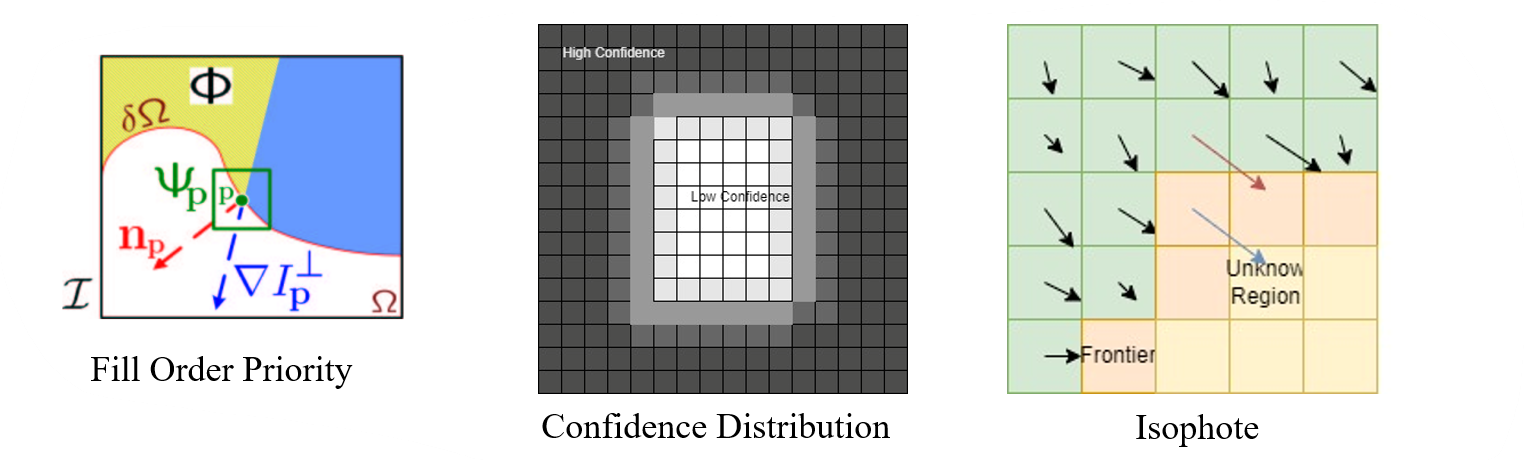
Find pixel with maximum Priority:

Filling order is crucial to non-parametric texture synthesis. Thus Exemplar-Based Inpainting designing a fill order which encourages the propagation of linear structure, together with texture. The algorithm will fill the best priority first. The priority computation is biased toward those patches which are on the continuation of strong edges and which are surrounded by high-confidence pixels.

The priority $P(p)$$P(p)$ of a patch ${\Psi }_p$$Ψ_p$ centred at the point $p$$p$ for some $p\in \delta \Omega$$p∈δΩ$ defined as the product of two terms: $P(p)=C(p)D(p)$$P(p)=C(p)D(p)$ We call $C(p)$$C(p)$ the confidence term and $D(p)$$D(p)$ the data term, and they are defined as follows:

The confidence term $C(p)$$C(p)$ may be thought of as a measure of the amount of reliable information surrounding the pixel $p$$p$. The intention is to give preference to pixels that were filled early on (or that were never part of the target region). The data term $D(p)$$D(p)$ is a function of the strength of isophotes on the front $\delta \mathrm{\Omega }$$\delta\Omega$. It will propagate the linear structure to the target region, and broken lines tend to connect.

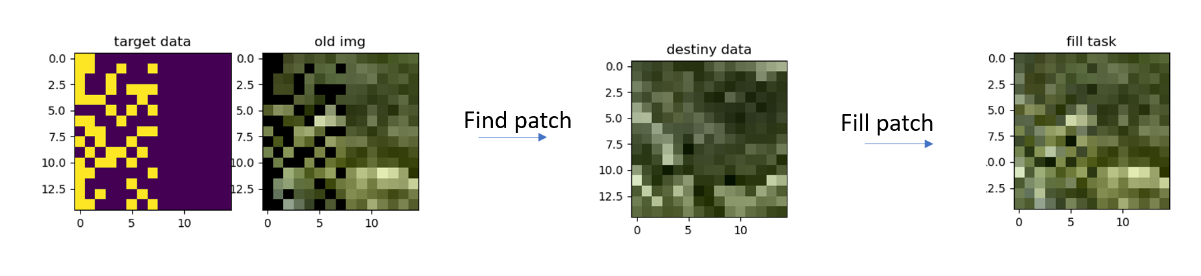
Find near and similar texture:

In the patch matching stage, this algorithm define the distance not only by SSD of two patches but also add the locality similarity as a heuristic. The assumption is that the neighbor patches may contain similar textures, and can avoid matching different objects far from the pixel $p^{\ast }$$p^*$

Using image patch around the mask do template matching (SSD)

This section introduces the scene completion algorithm to fill the rest region. Here users are allowed to input additional images similar to the original image. We then do template matching. We will use the patch around the mask as a template, denoted by $T$$T$. Using additional input matching image as $I$$I$. Notice that the mask region here should not affect the SSD score. So, we have a mask function as $M$$M$, which is 0 at the black region and 1 at the white region.

Using Poisson Blending to blend the best matching patch to the original image

In figure 1, the blue rectangle is the best-matching patch. Finally, as shown in figure, we will use Poisson blending to blend the best-matching patch to the template according to the mask.

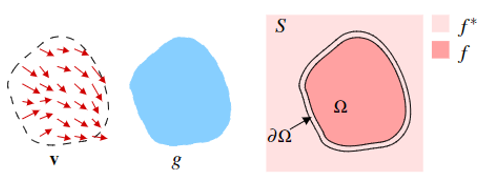
The process of blending is shown in Figure where $g$$g$ is ROI (Source),$v$$v$ is the gradient of $g$$g$, $f^{\ast }$$f^∗$ is the background image (Target), and $f$$f$ in $\mathrm{\Omega }$$\Omega$ is the function we want to solve according to $g$$g$ and $f^{\ast }$$f^*$. To calculate $f$$f$, we need to solve poissonmin equation . And Equation poisson kkt is the KKT condition for poissonmin equation. These two constraints produce us enough number of equations to construct a Linear system $Ax=b$$Ax=b$. Here $x$$x$ is the value of $f$$f$we want in $\mathrm{\Omega }$$\Omega$.

Results

References

• Boykov, Yuri Y., and M-P. Jolly. "Interactive graph cuts for optimal boundary & region segmentation of objects in ND images." Proceedings eighth IEEE international conference on computer vision. ICCV 2001. Vol. 1. IEEE, 2001.

• Criminisi, Antonio, Patrick Pérez, and Kentaro Toyama. "Region filling and object removal by exemplar-based image inpainting." IEEE Transactions on image processing 13.9 (2004): 1200-1212.

• Hays, James, and Alexei A. Efros. "Scene completion using millions of photographs." ACM Transactions on Graphics (ToG) 26.3 (2007): 4-es.

• Pérez, Patrick, Michel Gangnet, and Andrew Blake. "Poisson image editing." ACM SIGGRAPH 2003 Papers. 2003. 313-318.